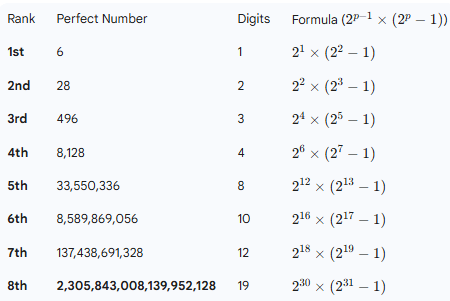
Explores perfect numbers, defined as positive integers equal to the sum of their proper divisors. Examples include 6, 28, and 496, with only 52 known today. It discusses mathematical properties, unsolved questions about odd perfect numbers, historical significance, and the connection to Mersenne primes, highlighting their allure across centuries.
The Goldbach conjecture, posed in 1742, asserts that every even number greater than 2 can be expressed as the sum of two prime numbers. Despite exhaustive verification for even numbers up to four quadrillion, no proof exists for all even integers. A million-dollar prize for a solution remains unclaimed.
Discusses the intriguing mathematical question of whether 196 is a Lychrel number, defined as a number that never results in a palindrome through repeated "reverse and add" processes. Despite extensive computational attempts, no palindrome has been found for 196, making it a leading candidate for a Lychrel number.
Explaining Science 