Roger Penrose’s cyclic model of the Universe makes use conformal mapping. This is a waybmapping from one set of coordinates to another which:
- preserves the angles at which lines meet and the shapes of infinitesimally small objects,
- but the sizes of objects are not preserved.
Conformal mapping, which had previously been confined to the realm of abstract mathematics, was made popular in the mid-twentieth century in drawings by the Dutch artist MC Escher.
Example of a conformal mapping in two dimensions
Consider an infinite plane, any point on the plane may be represented by polar coordinates (r, θ) where r is the distance from the origin and θ is the angle from the x-axis.

The infinite plane can be conformally mapped onto a circle which has radius =1 by defining new coordinates (R, Θ) where R = (er -1) / (er +1) and Θ = θ.
The diagram below shows how the infinite plane looks after the mapping. The boundary of the circle where R = 1 corresponds to a value of r = infinity
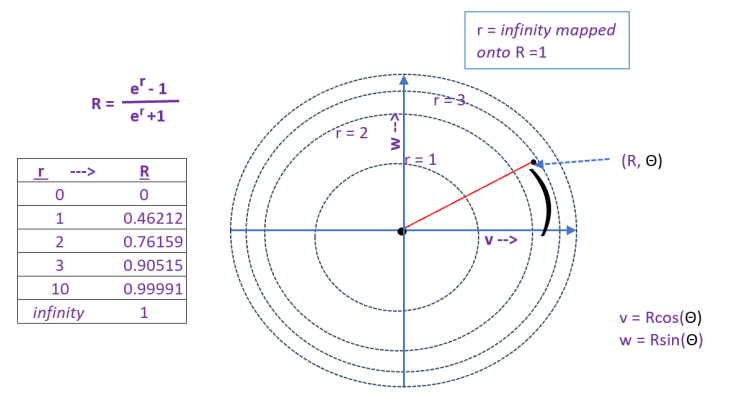
It can be shown (but I won’t do it here 😉) that the angles between any two lines are preserved by the conformal mapping from (r, θ) to (R, Θ). In general, only the shapes of infinitesimally small objects are preserved; the shapes of larger objects are not preserved and become distorted . The larger the shape the greater the distortion.
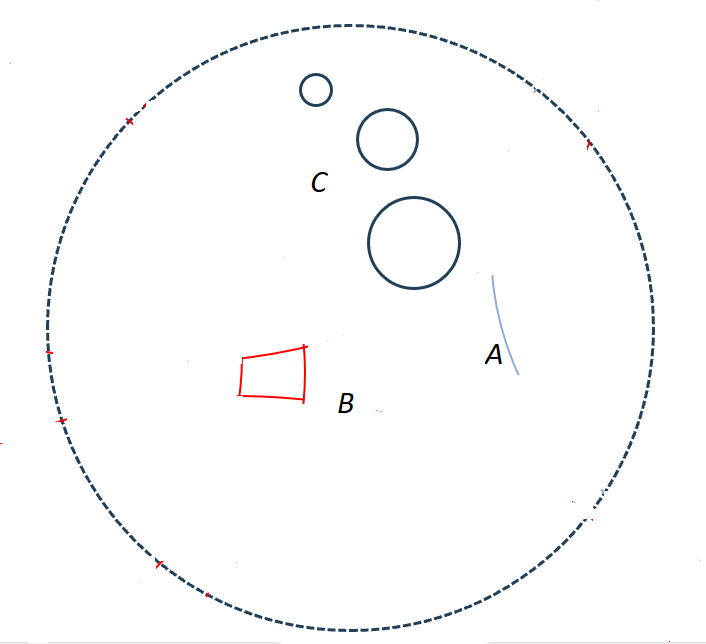
Some examples of how shapes are changed after the mapping.
- A straight line which does not pass through the origin becomes curved (A)
- The sides of a rectangle are distorted into curves (B)
- The shapes of circles are not distorted and remain as circles– but their sizes change. (C) shows how three circles of the same size appear after the mapping. The further the circle from the origin the smaller it is
Penrose diagrams
An earlier use of conformal mappings, long before Penrose developed the cyclic model of the Universe, is in Penrose diagrams. He developed these in the 1960s and they use a conformal mapping to show an infinite range of space and time on finite sized two-dimensional diagram. This makes them a very useful tool in cosmology for modelling the evolution of the Universe. For more details on how they work see the following:
