Is the Universe curved?

In this post I’ll talk about curvature, what terms such as flat, positive and negative curvature mean and how this applies to the Universe. I won’t use complex mathematical definitions here, but intuitively curvature is a measure of how much a two-dimensional surface deviates from being flat. This concept can be extended to any number of dimensions.

A flat space

Euclidean space is the most common example of a space which isn’t curved. It is the familiar space to which the rules of geometry taught at high school apply. For example, the angles of a triangle all add up to 180 degrees, Pythagoras’s theorem applies, and the area of a circle is πr².

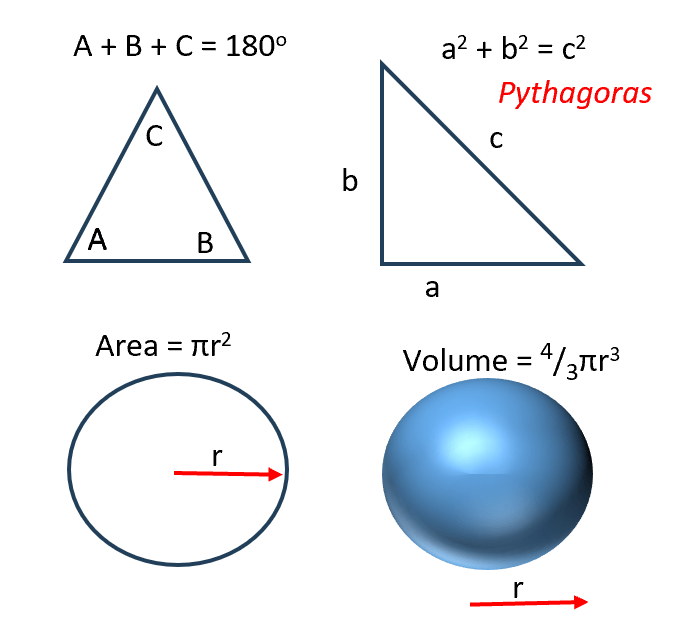
Euclidean space is infinite in extent and has no edge or boundary. In the abstract world of mathematics, it can have any number of dimensions. However, because we live in a world with three spatial dimensions, any space which has more than three dimensions is very difficult to visualise. For this reason, most people only think about examples of Euclidean space having three dimensions, which is the normal everyday space we appear to inhabit, or two dimensions which is a plane.

Positive curvature

Like Euclidean space, a positively curved space can have any number of dimensions. The most familiar example of a two dimensional positively curved space is the surface of a sphere.

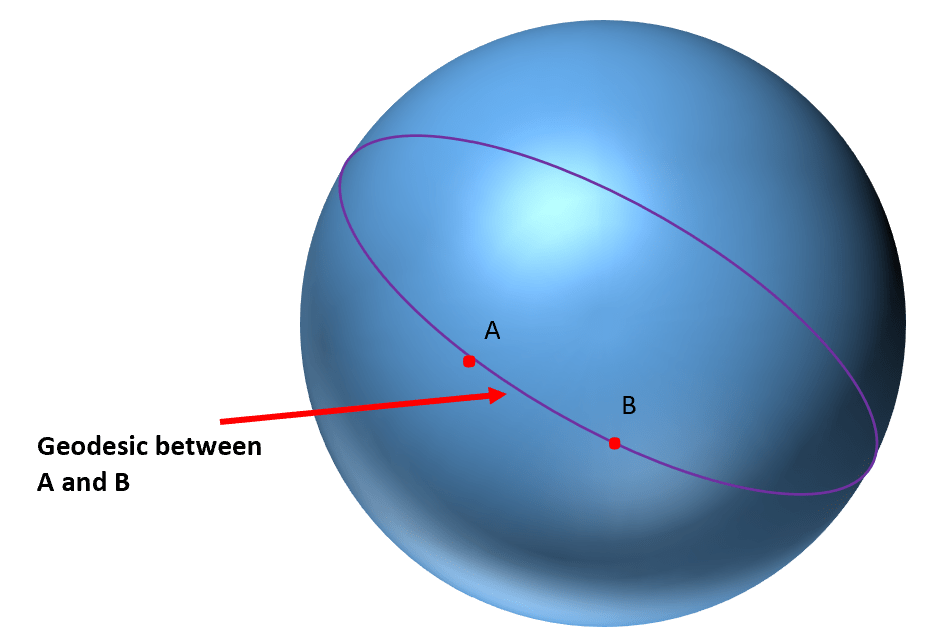
Because the surface of a sphere is curved, we have to re-define what we mean by a straight line. The equivalent of a [Euclidean geometry] straight line on the surface of a sphere is a curve called a geodesic. A geodesic is part of a great circle, a curve which passes around the sphere and is its full circumference in length.

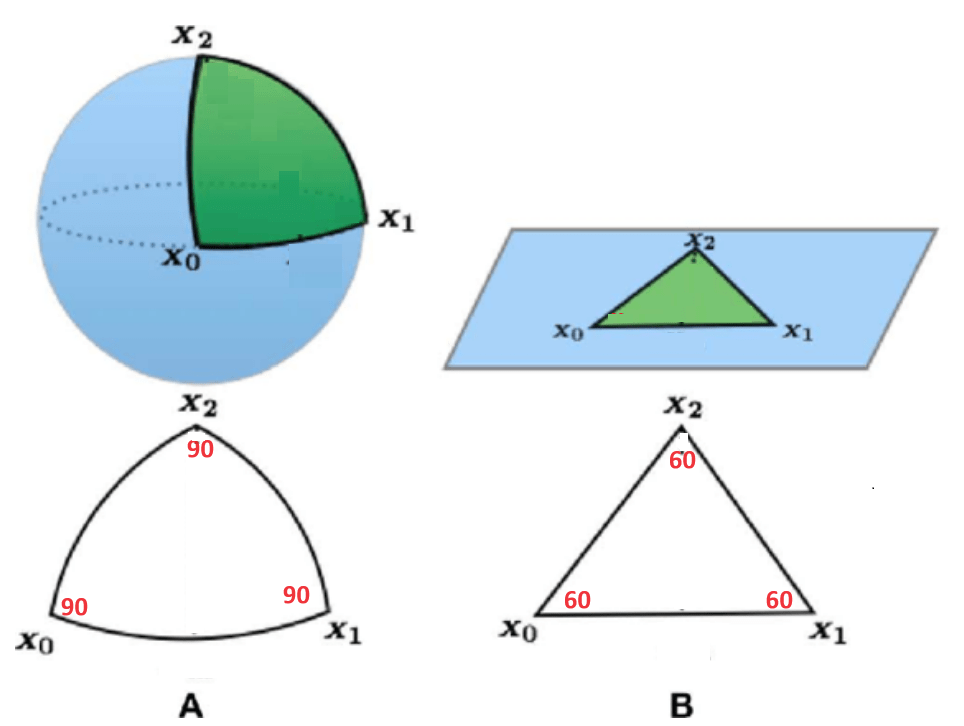
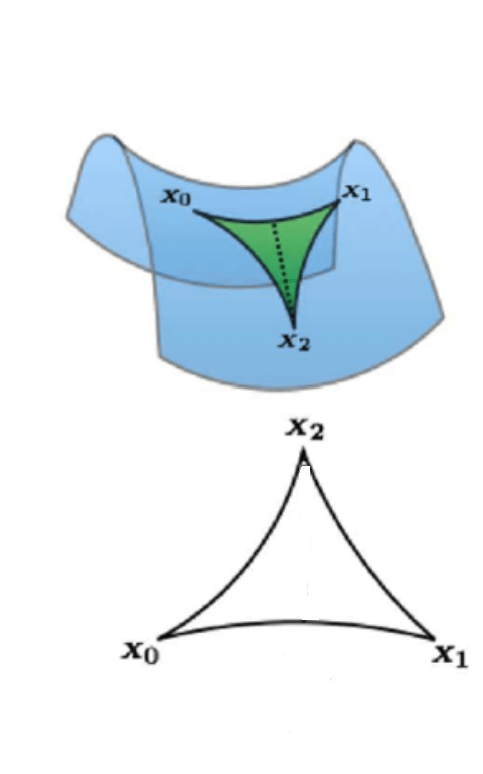
In the positively curved geometry on the surface of a sphere (A), the angles of a triangle add up to more than 180 degrees. For example, if we assume the Earth is a perfect sphere, which it nearly is, and we draw a large triangle on the surface of the Earth with:

• one corner on the equator and at zero degrees longitude (x₀)
• the second corner on the equator at 90 degrees east longitude (x₁) and
• the third corner at the North Pole (x₂),

 then the angles of this triangle add up to 270 degrees.

In general, the smaller the triangle in the relation to the radius of the sphere, the closer the sum of the angles is to 180 degrees. For example, if we constructed an equilateral triangle on the Earth’s surface whose sides were 1 km long, the sum of the angles would add up to 180.000 000 706 degrees.

Similarly,  if we draw a circle of radius r on the surface of a sphere, its area is more than the area given by the formula πr², which applies in Euclidean geometry The larger the radius of the circle r compared to the radius of the of sphere, the bigger the departure of the area of the circle from πr².

Measuring curvature

If we imagine a small creature like an ant crawling on a large spherical surface, such as the surface of the Earth, it would appear flat. Whereas a much smaller spherical surface such as the surface of a soccer ball would clearly be curved.

Mathematicians define the curvature of the surface of a sphere as 1/R² where R is the radius of the of sphere.

So the smaller the sphere the greater its curvature. For example

• The curvature of a soccer ball of radius 0.22 metres is 20.66 m^-2
• The curvature of the Earth, which has radius 6 371 000 metres is 0.000 000 000 000 024 6 m^-2

Even though it has no boundary the surface of sphere is a closed. If we continue in a straight line from any given point (which on the curved surface of the sphere means following a great circle) we will end up where we started from.

Positive curvature in three dimensions

If the Universe is positively curved, since it has three spatial dimensions, it means that it can be considered as a three-dimensional hypersurface on a hypersphere (a four-dimensional sphere). Because four-dimensional objects such as a hypersphere are difficult to visualise, illustrations of what is meant by positive curvature generally show a two-dimensional curved surface.

If the Universe is positively curved, then.

• The angles of a triangle add up to more than 180 degrees. However, for this to be detectable a triangle would have to be significant in size in comparison to the radius of the Universe.
• The area of a circle would be more than πr²
• The volume of a sphere would be more than ⁴/₃πr³
• The Universe is closed and has a finite volume. In theory if you had a straight ruler which was long enough (and it would have to be hundreds of billions of light years long!), the curvature of the Universe would mean it would arrive back at its starting point.

But it is not true that a space traveller (who could live for hundreds of billions of years !!) travelled in a straight line for long enough they would arrive back at their starting point. This is because the Universe is expanding, and the rate of expansion is increasing As they continued their journey, the distance they would need to travel to get back to their starting point would be continually increasing.

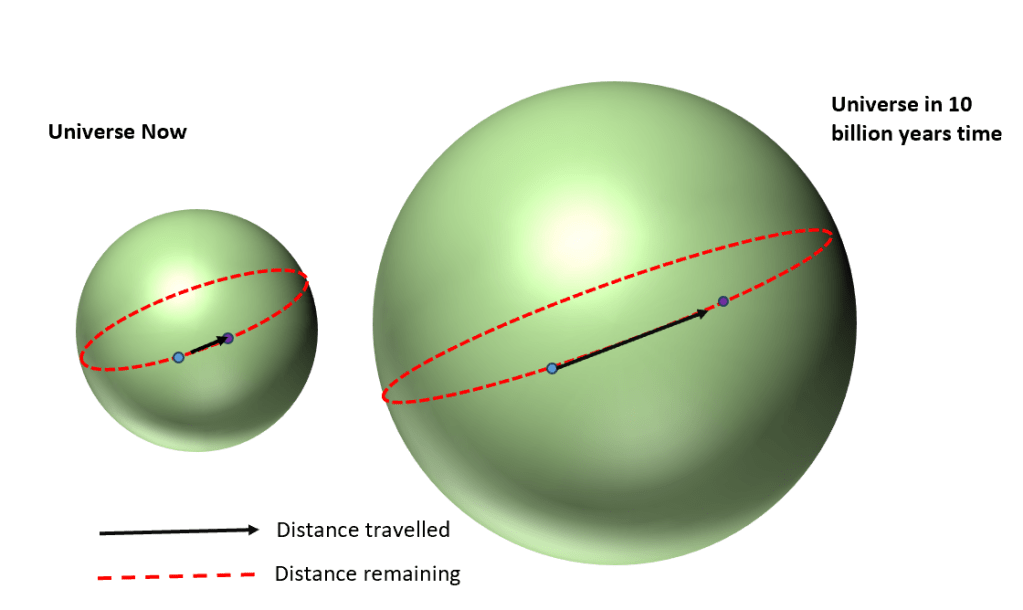
As the traveller continues their journey on a geodesic, no matter how fast they travel, the distance remaining on the journey always increases. This is illustration only shows the picture in two dimensions.

Negative curvature

Space can also be negatively curved. An example of a negatively curved two-dimensional surface is the hyperbolic plane – part of which is shown below. Because of its shape it is commonly called a saddle.

---

 The geometry on this surface is called hyperbolic geometry. In hyperbolic geometry the equivalent of straight lines in Euclidean geometry are also called geodesics. A hyperbolic plane has a property called the pseudo-radius, which is analogous to the radius of a sphere.  The larger the pseudo-radius the less curved the surface is.

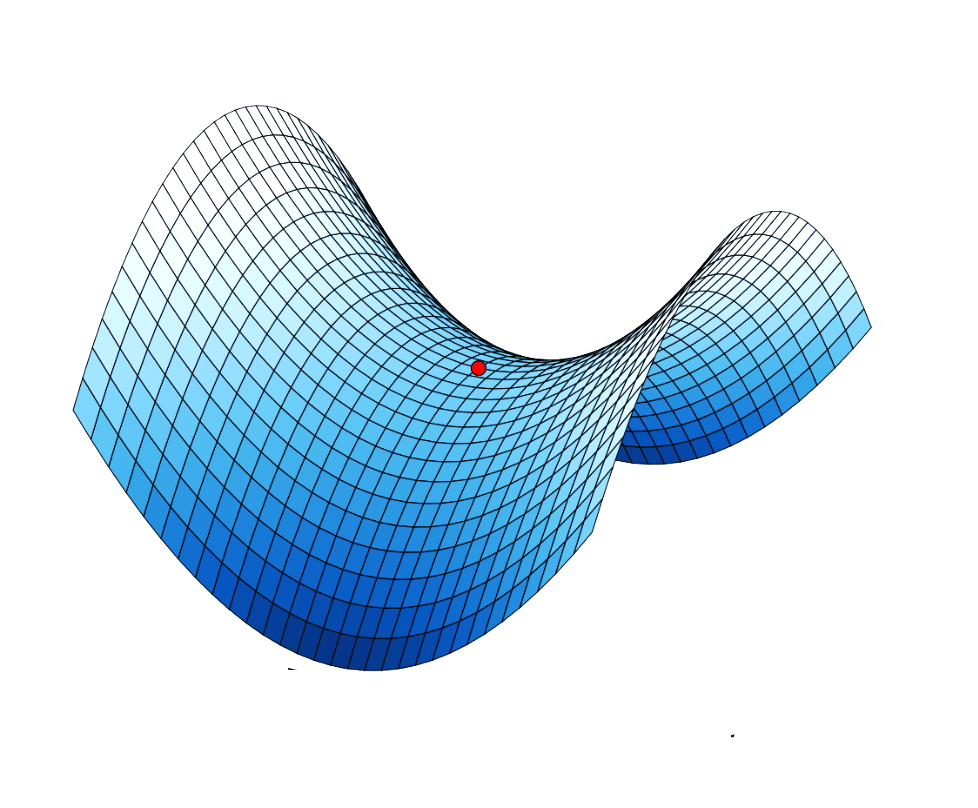
A hyperbolic plane with a small pseudo-radius (above) is more negatively curved than a hyperbolic plane with a large pseudo radius (below).

On a hyperbolic plane, the angles of a triangle add up to less than 180 degrees. The smaller the triangle in the relation to the pseudo-radius the closer the sum of its angles to 180 degrees.

Similarly, if we draw a circle of radius r on a hyperbolic plane, its area is less than πr². The larger the radius of the circle r compared to the pseudo-radius of the hyperbolic plane the bigger its departure from πr².

A hyperbolic plane like two-dimensional Euclidean space, but unlike the positively curved surface of the sphere, is always open, meaning that it is infinite in extent.

Negative curvature in three dimensions

If the Universe is negatively curved, then it is the three-dimensional analogue of the hyperbolic plane. This is sometimes called a hyperbolic hyperplane. (From a pure mathematical point of view this is not necessarily correct there are other hypersurfaces which have negative curvature). If this is the case

• The angles of a triangle add up to less than 180 degrees. However, for this to be detectable a triangle would have to be significant in size compared to the pseudo-radius of the Universe.
• The area of a circle is less than πr²
• The volume of a sphere is less than ⁴/₃πr³
• The Universe would be open and infinite in volume.

Is the Universe flat, positively curved or negatively curved?

The answer to this question is we don’t know. The curvature of the Universe depends on the density of the matter and energy in the universe. Cosmologists define a critical density (ρ_c). The value of ρ_c is 9.47 x 10^-27 kilograms per cubic metre. This is an incredibly small number – equivalent to about five atoms of hydrogen per cubic metre. For comparison, interplanetary space around the Earth, which is usually considered to be vacuum, has a density about a million times higher.

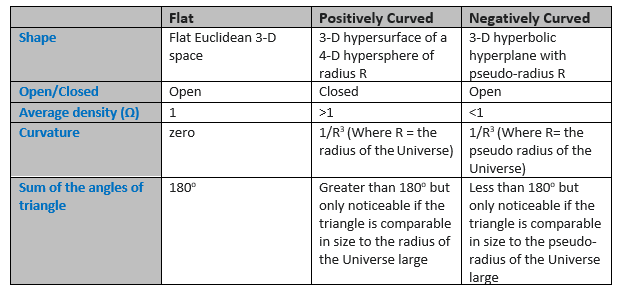
• If the average density is greater than ρ_c then the Universe has a positive curvature and is closed i.e., finite in extent.
• If the average density is equal to ρ_c   then the Universe is flat and open i.e., infinite in extent.
• If the average density is less than ρ_c then the Universe has negative curvature and is open.

Because the density of the Universe is such a small number in standard units, cosmologists use the symbol Omega (Ω) to indicate the ratio of the average density of the Universe to the critical density ρ_{c .} Therefore:

• if Ω = 1 we have a flat Universe
• if Ω > 1 a positively curved Universe and
• if Ω < 1 a negatively curved Universe.

 Current estimates (e.g. https://wmap.gsfc.nasa.gov/universe/uni_matter.html) are that Ω = 1 to within a small margin of error. This means the Universe is either flat or, if it is positively or negatively curved, its curvature is so small that it is indistinguishable from being flat.

In summary

And finally… the flatness problem

Although Ω = 1 to within a 0.5% margin of error at the current time, the equations of general relativity which govern the Universe, imply that to be so close to 1 now, in the very early Universe Ω must have been incredibly close  to 1. This leads cosmologists to question how the initial density came to be so finely-tuned to the ‘special’ value of 1 and is known as the flatness problem.

---